Úlohy uzavřené s výběrem odpovědi
(multiple-choice, polynomické úlohy)
Úlohy uzavřené s vícenásobnou
správnou odpovědí
Tyto úlohy předpokládají u žáka volbu více správných odpovědí z nabízených možností. (Teoreticky lze samozřejmě uvažovat i o volbě vícenásobné nesprávné odpovědi. Tyto typy úloh se však v praxi téměř nikdy nepoužívají.) Na použití úloh s vícenásobnou správnou odpovědí je nutné žáky vždy předem upozornit. U úloh s výběrem jedné správné odpovědi je totiž výběr více odpovědí považován za chybu a žáci by bez předchozího upozornění i v úlohách s vícenásobnou správnou odpovědí volili jen jednu variantu.
Problémem u úloh s vícenásobnou odpovědí je jejich skórování. Vedle jednoznačně správně a jednoznačně nesprávné odpovědi totiž existují i odpovědi částečně správná a částečně nesprávné. Ke skórování je tedy možné přistoupit dvojím způsobem:
Podle zákona vše nebo nic se jako správná uznává jen jedna vyčerpávající odpověď, ve které budou uvedeny všechny správné varianty. Ta je hodnocena maximem bodů. Každá jiná odpověď, byť by v ní byla jen jediná chyba nebo jediný chybějící údaj, je považována za špatnou a je hodnocena jako nevyřešená - 0 bodů. Je to přístup jednoduchý, úlohy se tímto způsobem dobře hodnotí, ale je to přístup tvrdý a žáky je vnímán jako nespravedlivý.
Diferencovaný přístup k hodnocení úloh s vícenásobnou správnou odpovědí dovoluje zahrnout do hodnocení i částečně správné odpovědi. Postup vyhodnocení demonstruje následující příklad:
Které z uvedených hudebních nástrojů patří mezi tzv. dřevěné dechové nástroje?
a) hoboj
b) fagot
c) cembalo
d) saxofon
e) trubka
f) mandolína
g) klarinet
h) pozoun
Žák odpověděl např. takto:

Označme si nyní zeleně správné odpovědi a červeně nesprávné odpovědi na tuto testovou otázku:

Nyní přidělíme jeden pomocný bod za každou označenou správnou odpověď a jeden pomocný bod za každou neoznačenou nesprávnou odpověď:
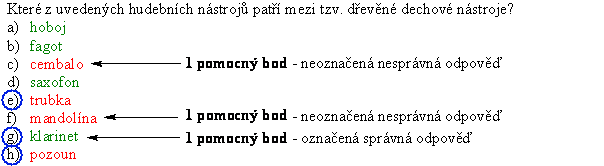
Celkový počet bodů za úlohu se získá jako podíl součtu pomocných bodů a počtu variant v testové úloze. V našem případě tedy 3:8. Žák tedy získává za takto vyřešenou úlohu 0,375 bodu. (Samozřejmě za předpokladu binárního skórování. Pokud by hodnotitel používal skórování vážené, pak by získaným koeficientem, v našem případě 0,375, musel vynásobit maximální počet bodů přidělovaný za danou úlohu.)

